Technologies used:
- Pyro
- PyQt5
- folium
- OSMnx
- NetworksX
- OpenStreetMap
- Geocoder
Description
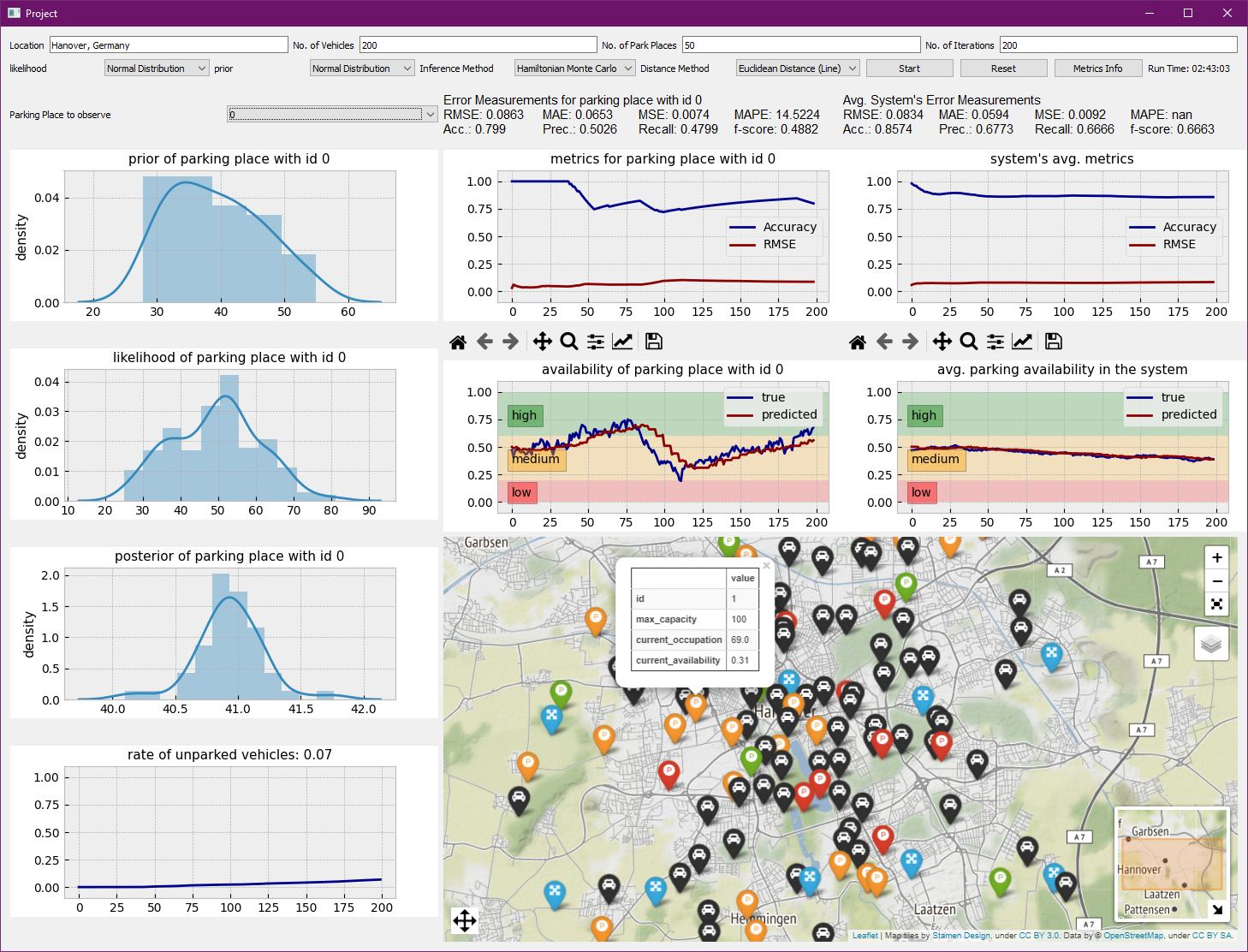
The application was developed as part of my Master’s thesis to apply the theoretical knowledge to a concrete use case.
The goal was to simulate traffic in a parking management system and try to predict the availability of parking vacancies using probabilistic programming (PP) methods.
PP deals with creating statistical models that represent the data-generating process and it specifies inference algorithms to infer properties of an underlying distribution of probability for these models. The main goal of PP is to find what is called the posterior distribution that represents the model data as well as possible, according to Van De Meent[1], this means: “a distribution of program inputs that could have given rise to the observed program output.”
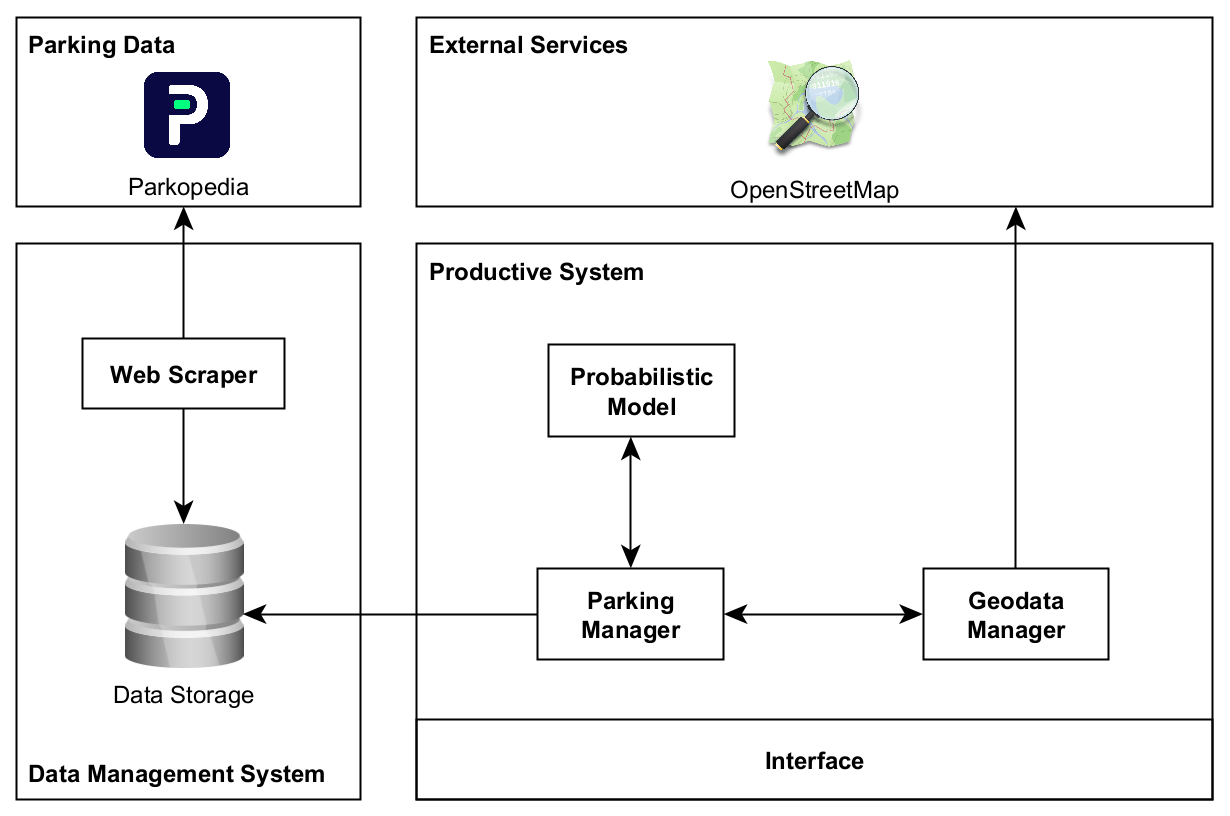
The system consists of multiple elements that are implemented using Python due to the compatibility to the Probabilistic Programming language Pyro. It is used to develop probabilistic models and forecast the parking availability based on collected or generated data. Data can be collected using the Web Scraping technique form parking reservation services like Parkopedia. The collected data can be stored in a database or any other readable format like CSV, TSV, or JSON to facilitate the querying process. The GUI is created using the library PyQt5 that allows using the C++ framework Qt for cross platform application development. For road map visualization Folium and OSMn are used. Folium is based on leaflet.js, an open-source JavaScript library for interactive maps, and it is responsible for plotting the map. OSMnx is responsible for routing, it can retrieve, model, analyze, and visualize OpenStreetMap (OSM) data (e.g., street networks) as NetworksX MulitDiGraph. Stats and distribuions plots are created using the library Matplotlib. The evaluation of the outcomes is done by the module (sklearn.metrics) of the Scikit library that provides functions to calculate different metrics.
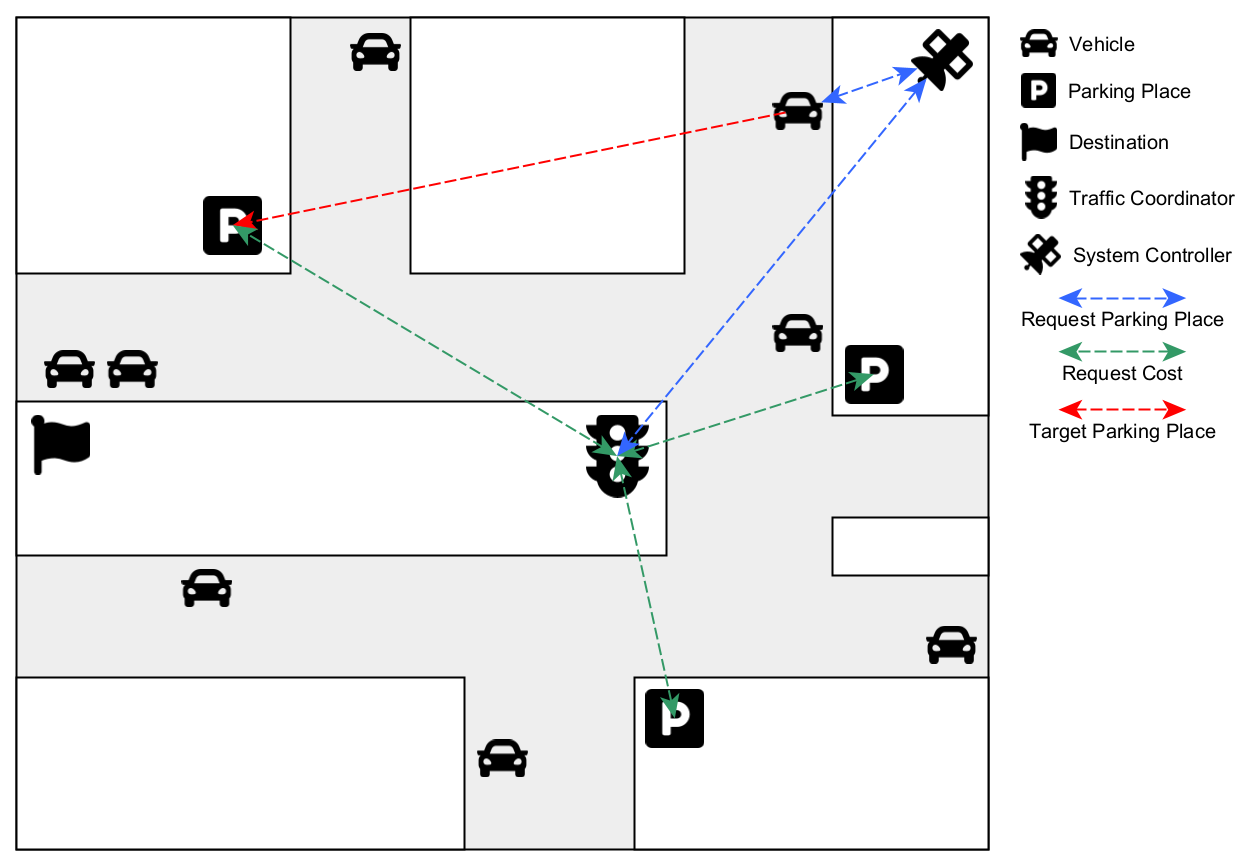
Each vehicle sends a request to the system responsible for assigning the best parking place for the desired destination. The system controller iterates through all Traffic Coordinators with Parking Places assigned to and determines the Traffic Coordinator with the shortest distance to the destination. The selected Traffic Coordinator propagates the vehicle data to it Parking Places that calculate the overall cost individually based on the following formula (inspired by the costs formula from [2]): (DV ∗ F + DD ∗ TV ) ∗ (1 − A)
Relating to the Parking Place, DV and DD are the distances to the vehicle and destination in meters, F is the fuel consumption, TV is the driver’s time value in a given currency, and A is the predicted availability by the Probabilistic Model in percent. The factors parking duration and parking fee are not considered in this calculation as they were in the original formula. The last term of the equation decides how much the current availability of parking vacancies affects the overall cost. This weighted factor increases the overall cost if the availability is low and decreases if the availability is high. The goal is not finding the cheapest but the optimal Parking Place to avoid overcrowding. The Parking Place with the lowest cost will be returned and assigned to the request sending vehicle. Now, the vehicle can start the simulated parking process by updating the Parking Place’s information about the current number of parked vehicles. The Parking Place checks whether there is enough capacity or not and returns a Parking State (boolean value) to the vehicle that indicates whether the vehicle got a parking place assigned or not. This value is propagated to the System Controller that updates its current knowledge about the Parking State of all parked and unparked vehicles in the system. At this moment, we assume all requests are made in a small time window, and no reservations can be made. The time costs of the driver and its companion can contribute to calculating the cost by multiplying it by the distance from the destination to the parking place. People with valuable time probably will not waste it by walking for a long time. Probably it would be more profitable for them to pay a higher parking cost. In this simulation, we will just consider one accumulated value representing the time value of the driver and its companion instead of assigning a value for each one and sum up these values afterward. It does not matter if one passenger has a time value of 40 or four passengers have a time value of 10.
Further details can be found in the abstract and are available on request.
[1] Jan-Willem Van De Meent, Brooks Paige, Hongseok Yang, and Frank Wood. An Introduction to Probabilistic Programming. Tech. rep. 2018. arXiv: 1809.10756v1. url : https://arxiv.org/pdf/1809.10756.pdf [2] Benhassine Sana, Harizi Riadh, and Mraihi Rafaa. “Intelligent parking management system by multi-agent approach: The case of urban area of Tunis”. In: 2014 International Conference on Advanced Logistics and Transport (ICALT). IEEE, May 2014, pp. 65–71. isbn: 978-1-4799-4839-0. doi:10.1109/ICAdLT.2014.6864084. url : http://ieeexplore.ieee.org/document/6864084/.